Graph Implementation

For C++ Implementation of Graph Abstract Data Types ADT:
 
The Graph Template Library - Stable branchhttp://freshmeat.net/projects/thegraphtemplatelibrary/
 
based on STL, Standard Template Library
 
Java Implementation
 
 
 
based on SWING.

Comments

Post a Comment

Popular posts from this blog

Ubuntu Remote Desktop to Windows Server

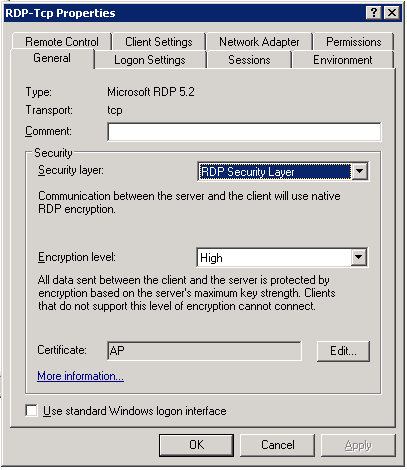
Image
On your Ubuntu machine, open Terminal Server Client or tsclient, install if not available, using sudo apt-get install tsclient Try giving RDPv5. If unable to get through, you need to change the Terminal Server Settings on Windows Server 2003 R2 machine. Go to Control-Panel->Administrative Tools->Terminal Services Configuration->Connections->RDP-Tcp. Right click for properties. In General tab, under security frame, from the dropdown combo having Security Layer, select RDP Security Layer. If it have SSL, you may not be able to connect from Ubuntu machine, but would be able to go from Windows machine. Below is the snap
Read more

Imote2 with Camera setup IMB400 over Ubuntu 9.10/10.04

Imote2 Camera driver for TinyOS is available in contribution directory of  TinyOS 2.x . It goes by the name of  tinyos-2.x-contrib . Its location within is  tinyos-2.x-contrib/intelmote2/apps I am assuming that you have tinyos-2.1.1 installed, this is required to have Camera Driver build. If you dont have it installed... than better have it done by invoking: apt-get install tinyos-2.1.1 From here on to get the driver working,  the procedure is as follows: Browse to opt directory. cd /opt The recommended way to get the source of tinyos-2.x and tinyos-2.x-contribis is through CVS. echo "Getting TinyOS 2.x and TinyOS 2.x-contrib from CVS" echo "Press enter when asked for password." cvs -d:pserver:anonymous@tinyos.cvs.sourceforge.net:/cvsroot/tinyos login cvs -z3 -d:pserver:anonymous@tinyos.cvs.sourceforge.net:/cvsroot/tinyos co -P tinyos-2.x cvs -z3 -d:pserver:anonymous@tinyos.cvs.sourceforge.net:/cvsroot/tinyos co -P tinyos-2.x-contrib --OR--  e...
Read more

Compilers ::: Begineers Guide ::: Developer Tools ::: Articles ::: Assessments

Image
IDE's and Compilers:::   Get ahead of Turbo C/C++ 3.0 IDE. Try these compilers   Free Integrated Development Environment for the C/C++ Mingw compiler (included with the package). http://www.bloodshed.net/devcpp.html http://ftp1.sourceforge.net/dev-cpp/devcpp4.zip http://ovh.dl.sourceforge.net/sourceforge/dev-cpp/devcpp4990setup.exe Snippet Compiler for    C#, VB.NET and ASP.NET http://www.sliver.com/dotnet/SnippetCompiler/ http://www.sliver.com/dotnet/SnippetCompiler/SnippetCompiler.zip   Beginners  Guides:::   Excellent guides for Beginners to  Jump start on following tools   Beginners  Guide to Develop C/C++ Projects Using Visual C++ # Dive Into Microsoft Visual C++ 6 (360K PDF)  http://www.deitel.com/books/cppHTP4/DiveIntoVCPP6.zip   Beginners  Guide to Develop C/C++ Projects Using Visual C++.NET # Dive Into Microsoft Visual C++ .NET (1.2MB, DRAFT PDF in ZIP file) http://www.d...
Read more